LaTeX is the best choice to create beautiful looking math documents. It provides easy typesetting for math formulas and handles the formatting for you. In this guide, we hope to give you your first introduction to LaTeX. We will talk about the essential functions of LaTeX you need to know to produce your first typeset homework.
There are two things you should do first:
Overleaf. Visit overleaf.com and create an account. This is a free online tool so nothing needs to be installed on your device.
A template. If your instructor provides a template, that is great. If not, you can also download one here.
After creating a new project on Overleaf, you will be directed to a work page. On the left side is a file directory (1).
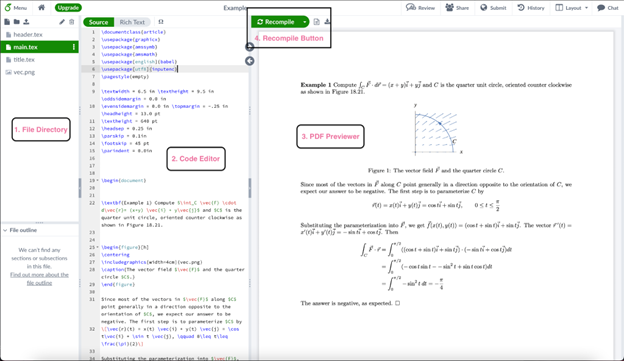
You can upload files or create new files here. In the middle is where you write the LaTeX code, which we will learn later in the tutorial (2). The right side is a preview of your document (3). Any moment when you want to see the progress of your file, you can click the recompile button to preview the pdf, as long as there are no errors in the code (4).
Now upload the template or copy paste the code to the main.tex file created with the project. If there are other auxiliary files included in the template, make sure to upload them as well.
\documentclass{article} #Preambles
\usepackage{graphicx}
\usepackage{amssymb}
\pagestyle{empty}
\begin{document}
First document. This is a simple example.
\end{document}
Let us start by understanding the template file. Find the \begin{document} and the \end{document} command. The content of the document should be enclosed inside the two tags. This is known as the body of the document. Text that uses the English alphabet can be typeset normally. Math symbols should be included in $...$ or in \[...\], which we will elaborate later.
You will notice that there are also commands before the \begin{document}; they are called preambles. What they do essentially is to determine the page setup such as margins, fonts, and page numbering of the document. The preambles are taken care of by the template, so we do not need to make changes to this part.
Unlike Microsoft Word, in LaTeX there is not a visual interface to help format the text. Instead, you want to write commands that tell the PDF compiler what to do. Commands often follow the syntax of \command{option}. To get a sense of how they work, let us look at some simple text formatting commands.
\textbf{...} command.\textit{...} command.\underline{...} command.An example of each of these in action is shown below:
Some of the \textbf{greatest}
discoveries in \underline{\textit{science}}
were made by \textit{accident}.
The above is rendered by LaTeX as:
The main attraction of LaTeX is its ease to work with math expressions. We are going to look at the two ways that you can insert your math expressions to the test: inline mode and display mode. The inline mode is used to write formulas that are part of a text. Here is an example:
Let $a$ and $b$ be integers with $b>0$. Then there exist unique integers $q$ and $r$ with the property that $a=bq+r$, where $0 \leq r \leq b$.
And here how the above code is rendered by LaTeX:
We want to include the math expressions in $...$. Equivalently, we can use \( ... \), or \begin{math} ... \end{math}. They all function the same. In the math environment, LaTeX will italicize the letters and identify the math symbols.
Displayed equations are independent from the surrounding text and are displayed in their own lines. It is often used for more important equations. Here is one example:
Let $(G,*)$ be a group, the center of $G$, written as $Z(G)$ is defined as
\[Z(G) = \{g\in G|gh=hg, \forall h\in G\}.\]
which ends up looking like:
Above, \[...\] is used for the display math mode. Equivalently you may also use \begin{displaymath}...\end{displaymath}, or \begin{equation} ... \end{equation}.
Notice in the first case that we have used > and \leq, which are the > and \(\leq\) signs. The symbol > can be found on our common keyboard, while \(\leq\) cannot. So we need to use the \leq command to represent it. To learn the commands for other symbols, here is a website that may be helpful to you. Try to memorize the commands for symbols that are common in your course.
We might want to use the list function when stating a theorem, or separating a proof into parts. You can create lists using a list environment. Environments are sections of our document that you want to present in a different way to the rest of the document. They start with a \begin{...} command and end with an \end{...} command. As we have seen above, all the content of the document is written inside the document environment.
An equivalence relation on a set $S$ is a set $R$ of ordered pairs of elements of $S$ such that
\begin{enumerate}
\item $(a,a)\in R$, $\forall a \in S$
\item $(a,b)\in R$ implies $(b,a) \in R$
\item $(a,b) \in R$ and $(b,c) \in R$ imply $(a,c)\in R$
\end{enumerate}
If you want your list to be unordered, you can also use the itemize environment:
An equivalence relation on a set $S$ is a set $R$ of ordered pairs of elements of $S$ such that
\begin{itemize}
\item $(a,a)\in R$, $\forall a \in S$
\item $(a,b)\in R$ implies $(b,a) \in R$
\item $(a,b) \in R$ and $(b,c) \in R$ imply $(a,c)\in R$
\end{itemize}
The display mode is commonly used to show the development of an equation. This often requires multiple lines of space. We could use \[...\] for every line, but it cannot make sure that the equals sign is nicely aligned. To learn how to do this, you can reference this Overleaf page.
Some homework problems might require you to include a sketch. This is not hard:
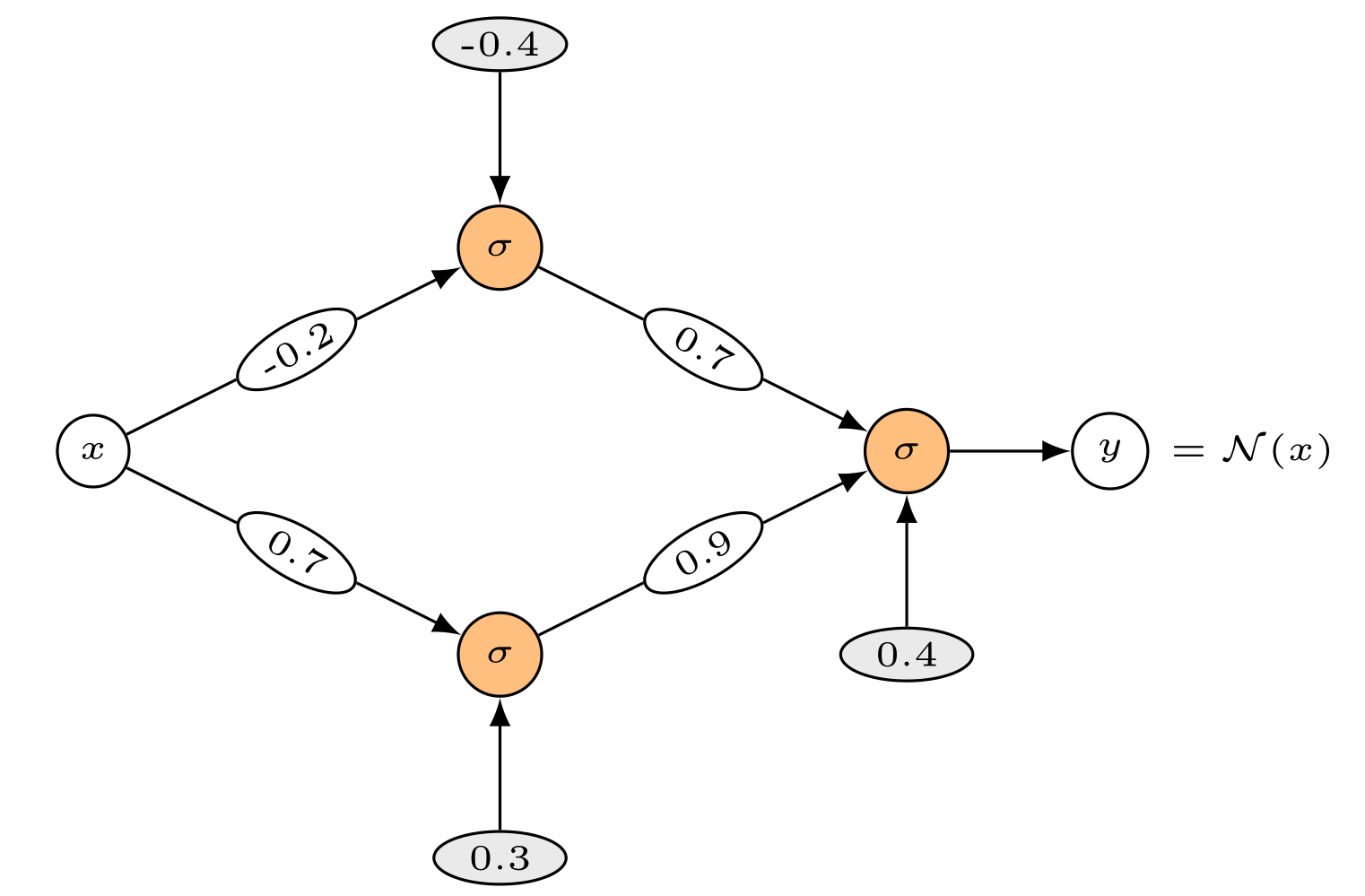
\includegraphics{neural_network}

But there are a couple lines you must include in the preamble first. See this Overleaf page on how to insert an image and then position it correctly within the document.
Superscript is used for expressions involving exponents, indexes, and in some special operators. For example to typeset \(a^4\), the command is $a^4$ and to typeset \(a_4\) the command is $a_4$. Here is an example that uses both subscripts and superscripts in interesting ways:
\[ \int_0^1 x^2 + y^2 \ dx \]
\bigskip
This command adds an empty line to the document. Use it when you want to add more spacing to the document or start a new line.
\medskip
Same as \bigskip, but for a smaller space.
\newpage
This command starts a new page.
\mathbb
This is the blackboard font used to typeset the real number symbol \(\mathbb{R}\). To typeset this symbol in LaTeX, use \mathbb{R}. The number sets \(\mathbb{Q}\), \(\mathbb{N}\), and others, can be typeset in a similar way.
\newcommand
Putting the line \newcommand{\cs}{def} somewhere in the preamble of the document defines a new control sequence \cs with definition def. As an example, the line \newcommand{\R} {\mathbb{R}} will allow you to type \R instead of \mathbb{R} anywhere in the document.
\noindent
When used at the beginning of the paragraph, it suppresses the paragraph indentation. It has no effect when used in the middle of a paragraph.
Here is a sample file which uses most of the functionalities mentioned above. Feel free to copy paste the code into your file to use some of the commands.
If you want to learn more about LaTeX, or need some formatting tools that are not mentioned above, feel free to reference the links below or the Overleaf website. Some quick links to common topics: