Math 3603: Advanced analysis #
Prof. Thomas Pietraho
Bowdoin College
Bowdoin College
The course begins by exploring the conversation between integration, measure theory, and probability, where the importance of generalizing the Riemann integral becomes apparent. We continue and study stochastic processes like random walks and Brownian motion, which require yet another type of integral defined by Kiyosi Itō. Mathematical finance is a natural application of this work, which we introduce in the waning weeks of the class.
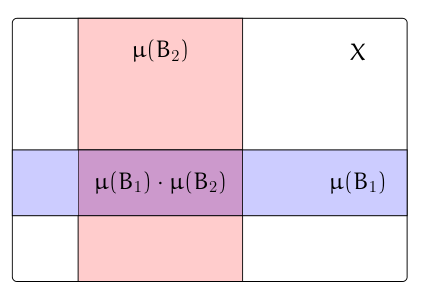
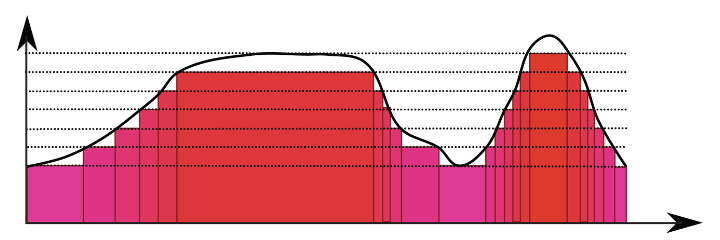
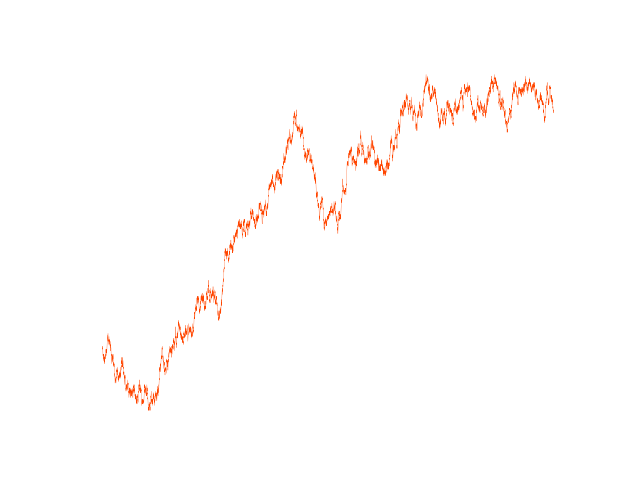
Course description: Measure theory and integration with applications to probability and mathematical finance. Topics include Lebesgue measure and integral, measurable functions and random variables, convergence theorems, analysis of random processes including random walks, Brownian motion, and the Itō integral.